Mathematical Modeling of Chakras: A Framework for Dampening Negative Emotions

Abstract

There are 114 chakras in the human mind, body, and sprit system. These chakras are the energy protocols for emotional, spiritual, and total well-being. This article explores different mathematical models of four specific non-linear chakras—Harsha, Vimarsha, Urja, and Sakshi—as a framework for mitigating the oscillations of negative emotions. Each of these four chakras has a distinct mantra, meditation, kriya, and yantra protocols for dampening the negative emotions. In this research work, for psychological impact analysis, we formulated different mathematical models for each chakra. We have used several empirical datasets to understand their functions.

Emotions play a pivotal role in human experience, influencing thoughts, behaviors, and overall well-being. Negative emotions, in particular, can lead to significant psychological distress and hinder personal development. By employing mathematical models that represent the interplay between these chakras and the intensity of negative emotions, we aim to provide insights into the dynamics of emotional regulation.

The framework utilizes a combination of exponential curves and Gaussian functions to illustrate the relationship between the non-linear chakras and emotional intensity balancing. This approach not only highlights the potential for emotional dampening through spiritual practices but also offers a novel perspective on integrating traditional wisdom with modern psychological insights.

Introduction

In the tradition of Sri Amit Ray, there are 114 chakras in the human body; among these, 64 are non-linear chakras, which are used for various spiritual awakenings and emotional balancing. The seven traditional chakras are linear and are not significantly related to emotional balancing.

While emotions are essential for navigating the complexities of life, the prevalence of negative emotions—such as anger, sadness, and fear—can significantly impact mental health and well-being. These emotions often manifest in oscillations, fluctuating in intensity and duration, leading to a cycle of emotional distress that can be challenging to manage.

In our tradition, among the 64 non-linear chakras, the Harsha chakra, Vimarsha chakra, Urja chakra, and Sakshi chakra protocols are very popular and often used for emotional balancing. Hence, in this article we focus on these four powerful balancing chakras.

We are in the process of modeling all the 114 chakras using different scientific modalities. Among these, modeling the third-eye chakra, the thousand petals crown chakra, and the 6 cosmic chakras are fascinating.  However, here we focus on the 4 behavioural chakras, together they are know as Sūkṣma Saṅghyam Tantu (सूक्ष्म संघ्यम तंतु ) chakra. 

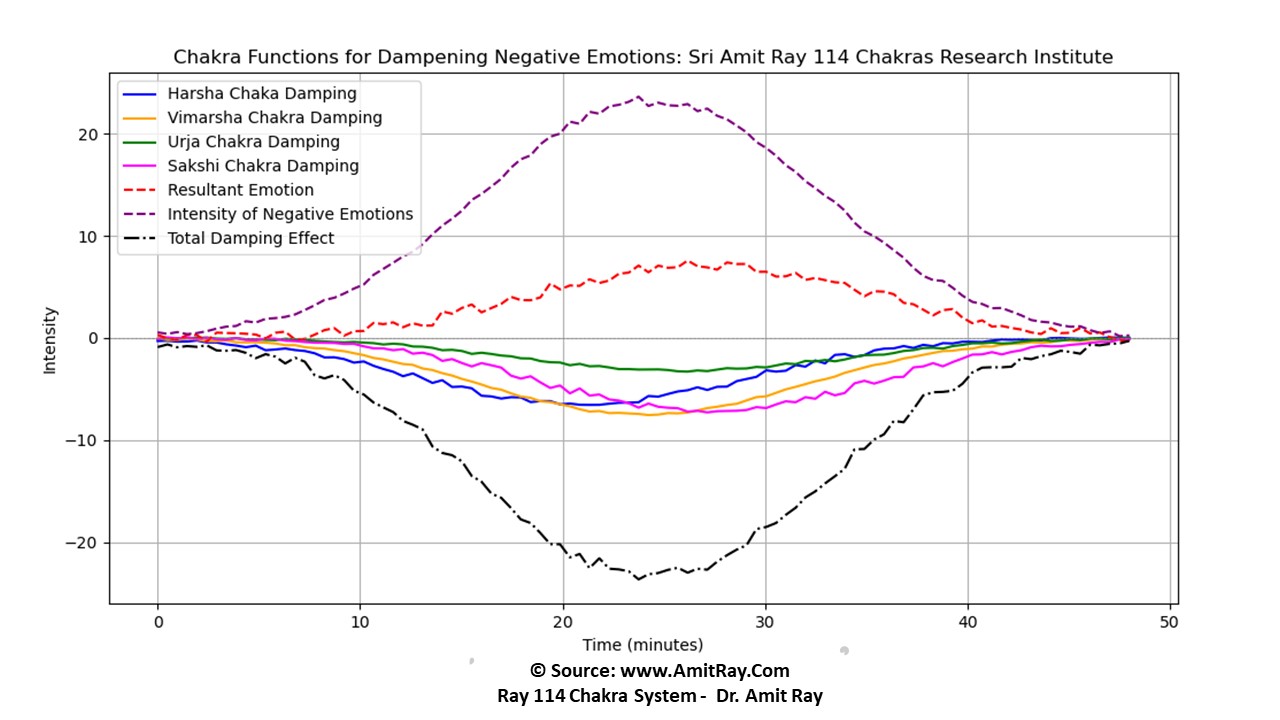
A model using the Harsha, Vimarsha, Urja, and Sakshi chakras to dampen emotional oscillations involves mapping these chakras to specific emotional regulation techniques that support stabilization, introspection, vitality, and witnessing. This approach incorporates chakra-based mantra, meditation practices, kriyas, and visualization techniques that target specific areas of consciousness and resilience. We have used three sets of protocols for each chakra. 

Here’s how these chakras can be used in a structured framework for regulating emotional oscillations:

Chakra Overview and Emotional Regulation Roles

  • Harsha Chakra (Chakra of Joy): Located near the heart, Harsha chakra is associated with joy, positivity, and emotional openness. Activating this chakra helps to counteract negative emotions by fostering a state of joy and reducing the overall intensity of negative fluctuations.
  • Vimarsha Chakra (Chakra of Insight): This chakra is linked with introspection and self-reflection. Engaging Vimarsha chakra facilitates understanding and processing of negative emotions, thereby helping to bring clarity and reduce reactivity.
  • Urja Chakra (Chakra of Vitality): Associated with physical and emotional energy, this chakra provides the stamina required to face emotional challenges. By tapping into Urja, one can build resilience, making it easier to withstand and regulate emotional waves.
  • Sakshi Chakra (Witness Consciousness Chakra): This chakra promotes detachment and witnessing, allowing one to observe emotions without being overtaken by them. Activating Sakshi enables a calm, observing state, which is critical for reducing emotional oscillations by limiting reactive engagement.

2. Non-Linear Emotional Dampening Model Using Chakra Activation

The model introduces each chakra as a damping function that influences the oscillatory behavior of negative emotions. Here’s how each chakra can be mathematically represented and applied within a non-linear system:

The model presents a novel approach to understanding how chakra activation can serve as a damping mechanism for negative emotions. Each chakra is conceptualized as a damping function, contributing to the modulation of emotional oscillations. By mathematically representing these chakras, we can illustrate their individual and collective impacts on emotional states. This section will detail how each chakra can be integrated into a non-linear system to dampen negative emotional intensity.

2.1 Chakra Activation as Damping Functions

In the context of our model, each of the Harsha, Vimarsha, Urja, and Sakshi chakras can be represented using specific mathematical functions that reflect their unique properties and influences. The general form of these functions is designed to exhibit non-linear characteristics, capturing the complexity of emotional responses:

  1. Harsha Chakra: This chakra is associated with joy and positivity. Its damping function can be modeled as an inverted Gaussian curve, which represents the ability of positive energy to reduce the intensity of negative emotions. Mathematically, this can be expressed as:

H(t) = A_H e^{-\frac{(t - t_H)^2}{2\sigma_H^2}}

where A_H is the amplitude, t_H is the time of maximum activation, and \sigma_H controls the duration of the effect, the width of the curve.

  1. Vimarsha Chakra: Linked to self-awareness and introspection, the Vimarsha chakra can be represented by a U-shaped exponential function. This reflects how deep introspection can lead to profound realizations that mitigate negative emotions. The function may be defined as:

V(t) = A_V \left(1 - e^{-k_V (t - t_V)}\right)

where A_V is the amplitude, k_V is the rate of growth, and t_V denotes the point of maximum influence.

  1. Urja Chakra: Representing vital energy and motivation, the Urja chakra can be modeled similarly to the Harsha chakra but with distinct parameters. Its function could take the form:

U(t) = A_U e^{-\frac{(t - t_U)^2}{2\sigma_U^2}}

Here, A_U, t_U, and \sigma_U follow analogous interpretations, indicating the intensity, timing, and width of the emotional dampening effect.

  1. Sakshi Chakra: This chakra embodies observation and detachment. Its influence can be modeled through a sigmoid function, capturing the gradual realization and acceptance that dampens emotional spikes:

S(t) = \frac{L_S}{1 + e^{-k_S (t - t_S)}}

where L_S is the maximum value of the function, k_S dictates the steepness of the curve, and t_S signifies the midpoint of the emotional transition.

2.2 Integration into a Non-Linear System

To explore the overall impact of these chakra functions on negative emotions, we can formulate an integrated model that combines their effects. The intensity of negative emotions, represented by I(t), can be expressed as:

I(t) = I_0 - \left(H(t) + V(t) + U(t) + S(t)\right)

where I_0 represents the baseline intensity of negative emotions. The damping effect is a cumulative result of the individual contributions from each chakra function, reflecting their synergistic influence on emotional regulation.

2.3 Implications of the Model

This non-linear emotional dampening model provides a framework for understanding how chakra activation can mitigate negative emotions. By analyzing the mathematical interactions of the chakra functions, we can gain insights into potential therapeutic interventions. Such interventions may involve targeted practices—such as meditation, visualization, or energy healing—that focus on activating these chakras to enhance emotional resilience and promote psychological well-being. Further research and empirical validation of this model could pave the way for integrating ancient wisdom with modern psychological practices, fostering a holistic approach to emotional health.

3. Dampening Negative Emotions: A Mathematical Chakra Framework

Understanding and managing negative emotions is a key part of achieving emotional stability and well-being. In this framework, we explore the role of four specific chakras—Harsha, Vimarsha, Urja, and Sakshi—and how they contribute to dampening the oscillations of negative emotions through a mathematical approach. Each chakra provides a unique “damping function” that collectively helps reduce the intensity of negative emotional waves over time.

3.1 Emotional Intensity Function

Let’s denote the emotional intensity of negative emotions over time as:

I(t)

where I(t) represents the intensity of negative emotions at any given time t .

3.2 Combined Damping Equation

To describe the overall effect of damping on emotional intensity, we can combine the damping effects of the four chakras. The equation for this damping effect is as follows:

\frac{d^2 I}{dt^2} + \left( \zeta_{\text{Harsha}} + \zeta_{\text{Vimarsha}} + \zeta_{\text{Urja}} + \zeta_{\text{Sakshi}} \right) \frac{dI}{dt} + \omega^2 I = 0

where:

  • \frac{d^2 I}{dt^2} is the acceleration of the emotional intensity (second derivative of I ),
  • \zeta_{\text{Harsha}}, \zeta_{\text{Vimarsha}}, \zeta_{\text{Urja}}, \zeta_{\text{Sakshi}} are the damping coefficients of each chakra,
  • \omega is the natural frequency of emotional oscillations.

3.3 Chakra Damping Functions

Each chakra contributes a unique damping function that influences the rate at which negative emotions decrease. Here is how each chakra’s damping function is defined:

Harsha Chakra (Joy)

The Harsha Chakra introduces a joy-based damping effect, gradually decreasing in strength over time. The damping function for Harsha Chakra is:

\zeta_{\text{Harsha}}(t) = h \cdot e^{-\alpha t}

where h is the initial strength of joy and \alpha is the decay rate.

Vimarsha Chakra (Insight)

The Vimarsha Chakra provides an insight-based damping function that adjusts based on the current intensity of negative emotions. As insight grows, the emotional intensity is regulated more effectively:

\zeta_{\text{Vimarsha}}(t) = v \cdot \left( 1 - \frac{1}{1 + I(t)} \right)

where v is the strength of the insight-based damping.

Urja Chakra (Vitality)

The Urja Chakra supplies an oscillating vitality-based damping function, contributing rhythmic energy that affects the frequency of the emotional intensity:

\zeta_{\text{Urja}}(t) = u \cdot \sin(\beta t)

where u represents the amplitude of vitality and \beta is the frequency of oscillations.

Sakshi Chakra (Witnessing)

The Sakshi Chakra applies a witnessing or awareness-based damping, which grows over time as awareness develops:

\zeta_{\text{Sakshi}}(t) = s \cdot \left( 1 - e^{-\gamma t} \right)

where s is the strength of witnessing and \gamma is the rate of growth in awareness.

Total Damping Coefficient

The total damping effect from all four chakras can be expressed as the sum of their individual damping functions:

\zeta_{\text{total}}(t) = \zeta_{\text{Harsha}}(t) + \zeta_{\text{Vimarsha}}(t) + \zeta_{\text{Urja}}(t) + \zeta_{\text{Sakshi}}(t)

This total damping coefficient combines the contributions from joy, insight, vitality, and witnessing.

Overall Differential Equation for Emotional Intensity

By substituting the total damping coefficient into the initial damping equation, we get the overall differential equation for the emotional intensity function I(t) :

\frac{d^2 I}{dt^2} + \zeta_{\text{total}}(t) \frac{dI}{dt} + \omega^2 I = 0

This equation models the behavior of negative emotions under the influence of the four chakra-based damping functions. Over time, as each chakra’s damping effect contributes, the oscillations of negative emotions are progressively reduced, leading to a state of emotional stability and resilience.

4. Mathematical Functions of Emotions and Chakras

Mathematical functions can effectively model various aspects of emotions, including their intensity, duration, and interaction with different factors such as time and external stimuli. Below are some common mathematical models and functions used to represent emotions, particularly negative emotions.

1. Gaussian Function

The Gaussian function, often used in statistics, can represent the intensity of emotions [11], where the peak represents the maximum intensity of the emotion at a certain time. It is often used in a normalized form:

f(t) = A \cdot e^{-\frac{(t - \mu)^2}{2\sigma^2}}

Where:

  • f(t) is the intensity of the emotion at time t.
  • A is the amplitude (maximum intensity).
  • \mu is the mean (time at which the emotion peaks).
  • \sigma is the standard deviation (how quickly the emotion intensity falls off).

2. Inverted Gaussian Function

For modeling the dampening effect of emotional regulation or healing, an inverted Gaussian can be used:

g(t) = -A \cdot e^{-\frac{(t - \mu)^2}{2\sigma^2}}

Where the negative sign indicates a reduction in intensity over time.

3. Exponential Decay

An exponential decay function can model the fading of negative emotions over time:

h(t) = I_0 \cdot e^{-\lambda t}

Where:

  • h(t) is the intensity of the emotion at time t.
  • I_0 is the initial intensity.
  • \lambda is the decay constant, determining how fast the emotion fades.

4. Linear Function

A simple linear function can represent a steady change in emotion over time:

m(t) = mt + b

Where:

  • m is the slope, indicating the rate of change of emotion.
  • b is the initial value (intensity at time t=0).

5. Piecewise Functions

Emotional states can change abruptly; hence, piecewise functions can represent different phases of emotional intensity:

E(t) = \begin{cases} f_1(t) & \text{for } t_1 < t < t_2 \\ f_2(t) & \text{for } t_2 < t < t_3 \\ \end{cases}

6. Sigmoid Function

The sigmoid function can model the transition from one emotional state to another, representing how emotions can start small, grow, and then saturate:

s(t) = \frac{L}{1 + e^{-k(t - t_0)}}

Where:

  • L is the curve’s maximum value.
  • k is the steepness of the curve.
  • t_0 is the time of the midpoint.

7. Combination of Functions

To model complex emotional interactions, combinations of these functions can be used. For example, a sum of Gaussian functions can represent the interaction of multiple emotions:

C(t) = A_1 e^{-\frac{(t - \mu_1)^2}{2\sigma_1^2}} + A_2 e^{-\frac{(t - \mu_2)^2}{2\sigma_2^2}}

Example of Emotional Intensity Over Time

Consider the emotional intensity modeled as a combination of the inverted Gaussian and exponential decay functions:

I(t) = -A \cdot e^{-\frac{(t - \mu)^2}{2\sigma^2}} + I_0 \cdot e^{-\lambda t}

Application in Psychological Studies

These mathematical models can be applied in various psychological studies to:

  • Analyze the trajectory of emotions over time.
  • Study the effects of interventions (like therapy) on emotional intensity.
  • Predict emotional responses based on external stimuli or internal states.

Conclusion

This framework provides a mathematical approach to understanding how specific chakras contribute to regulating and dampening negative emotions. By focusing on joy, insight, vitality, and awareness, the combined damping effects create a pathway to emotional resilience and stability. Through the continuous practice of balancing these chakra energies, we can reduce the intensity of negative emotional experiences, leading to lasting well-being and emotional health.

References:

  1. Burigana, L., & Vicovaro, M. (2020). Algebraic aspects of Bayesian modeling in psychology. Journal of Mathematical Psychology, Vol.94.
  2. Busemeyer, J. R., & Diederich, A. (2002). Survey of decision field theory. Mathematical Social Sciences.
  3. Clark, J. E., Watson, S., and Friston, K. J. (2018). What is mood? A computational perspective. Psychol. Med. 48, 2277–2284.
  4. Knill, D. C., and Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719.
  5. Yanagisawa H. Free-Energy Model of Emotion Potential: Modeling Arousal Potential as Information Content Induced by Complexity and Novelty. Front Comput Neurosci. 2021 Nov 19;15:698252. doi:10.3389/fncom.2021.698252. PMID: 34867249; PMCID: PMC8641242.
Tags: