Quantum Computing with Many World Interpretation Scopes and Challenges

1. Many Worlds Interpretation Basics

In 1957, Hugh Everett proposes, Many Worlds Interpretation (MWI) of quantum theories. According to this theory,  the famous Schrödinger’s cat is alive in one world and is dead in another world.  In MWI Everett, avoids the issue of wave function collapse. MWI from the assumption that the universal wave function is a superposition of an extraordinarily large set of real, existing worlds. MWI applies the entire mathematical apparatus of quantum mechanics to the universe, whereas the wave function collapse theories are essentially limited to the microscopic domain. MWI framework can provide simultaneous access to many computational worlds. 

Everett suggests that, when a measurement is made for a system in which the wave function is a mixture of states, the universe branches into a number of non-interacting universes. Each of the possible outcomes of the measurement occurs, but in a different universe. Particles are entangled, space and time become one, and information exists simultaneously across multiple, or infinite universes. 

According to the MWI, Schrödinger equation applies at all times. In other words, that the wave function of the Universe never collapses. Hence, MWI is also known as collapse-free quantum theory.  There is only one wave function, and it evolves smoothly and deterministically over time without any kind of splitting or parallelism. MWI removes the observer-dependent role in the quantum measurement process by replacing wavefunction collapse with quantum decoherence. Decoherence shows how a macroscopic system interact with many microscopic systems. Here, all components of the wave function still exist in a global superposition. 

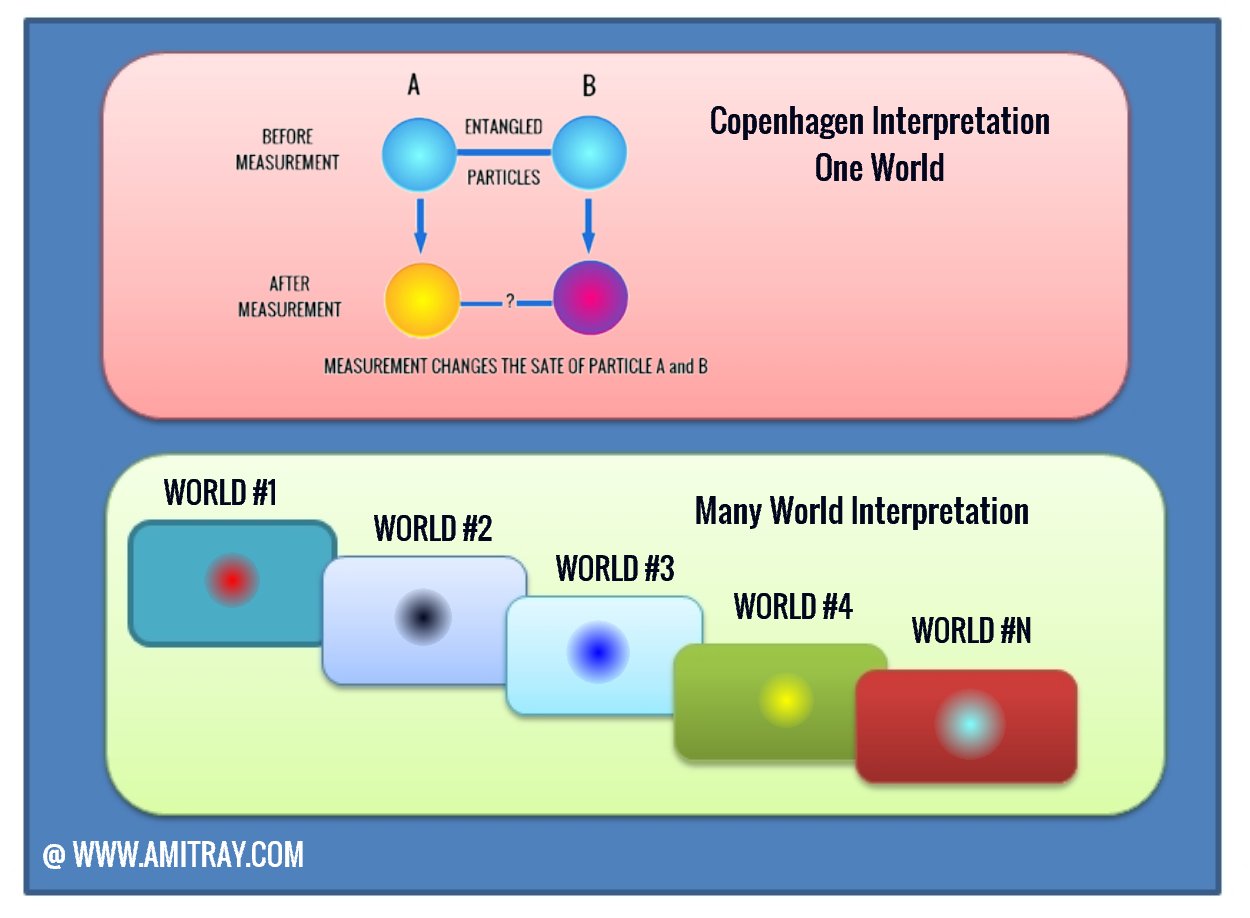
Everett’s many-worlds interpretation posited no collapse. Instead, probabilities bifurcate at the moment of measurement into parallel universes. Although an infinite number of un-testable universes seems unscientific to some, many physicists today view the theory as very important. For example, Tegmark called the many worlds interpretation “one of the most important discoveries of all time in science.” 

2. Limitations of Bohr’s Copenhagen Interpretation

Copenhagen interpretation holds that physical systems have only probabilities, rather than specific properties, until they’re measured. In Schrödinger’s thought experiment, a cat in a box is both dead and alive until it is seen. In Bohr’s words, the wave and particle pictures, or the visual and causal representations, are “complementary” to each other. That is, they are mutually exclusive, yet jointly essential for a complete description of quantum events.

The wave function is a complete description of the quantum state of a particle, and the Schrödinger equation describes the behavior of the wave function in space and time. The Schrödinger equation is a mathematical “wave equation,” i.e. a second-order linear partial differential equation. The set of all possible wave functions forms an abstract mathematical vector space called a “Hilbert space.” 

Paul Dirac famously proposed adding a postulate to the quantum mechanical framework that “a measurement always causes a system to jump into an eigenstate of the observed quantity.”  However, where and at what point the system “jumps” into an eigenstate – is entirely ambiguous with no scientifically precise definition. Max Born suggested, the square of the absolute value of the wave (ψ) function expresses a probability amplitude for the outcome of a measurement. Why the probability amplitude be square, not something else, it is not scientifically very well defined.

Einstein, however, persistently argued that the Copenhagen interpretation was incomplete. He conjectured that there might be hidden variables or processes underlying quantum phenomena; or perhaps ‘pilot waves’, proposed by de Broglie, govern the behaviour of particles.

David Bohm also argued that particles in quantum systems existed whether observed or not, and that they have predictable positions and motions determined by pilot waves. John Bell then showed that Einstein’s concerns about locality and incompleteness in the Copenhagen interpretation were valid. It was he who refuted von Neumann’s proof by revealing that it ruled out only a narrow class of hidden-variables theories.

3. Many-World Interpretation and Branches: 

The many-worlds interpretation is DeWitt’s popularisation of Everett’s work. The combined observer–object system as being split by an observation, each split corresponding to the different or multiple possible outcomes of an observation. These splits generate a possible tree and branches.

There are two versions of observer, one who has seen a dead cat, and the other who has seen an alive cat. These two versions cannot interact with each other, and will never be able to know of the other’s existence. When one observer open the box we say that the universe “branches.” Initially there was just one cat. But after the radioactive decay and cyanide release the universe branched into two “sub-universes”, one containing the dead cat and the other one containing the alive cat. These sub-universes are called branches, but they are also popularly termed “worlds”, hence the theory being called many worlds theory. 

4. Many World Interpretation Model

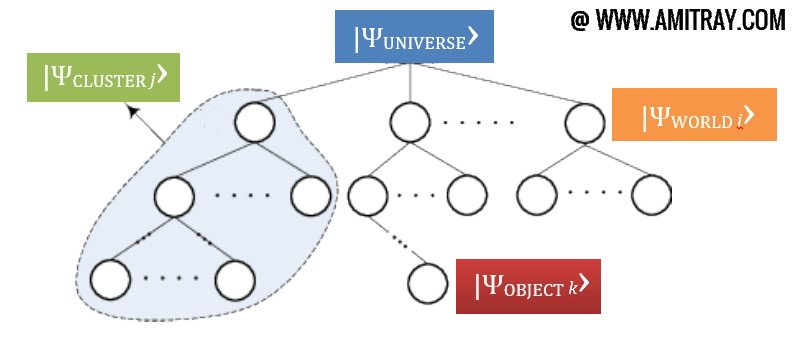
Many-worlds,  views reality as a many-branched tree, wherein every possible quantum outcome can be realized. There are several versions of many-world interpretations. The existence of the other worlds makes it possible to remove randomness and action at a distance from quantum theory and thus from all physics. Here, a world is the totality of macroscopic objects such as: qubits, gates, stars, cities, people, grains of sand, etc. in a definite classically described state. In MWI, an “observer” has no special status and so there is no such thing as a wave collapse. MWI is based on the simple assumption that the entire universe can be modeled by a universal wave function that obeys a deterministic wave equation. 

|Ψ_UNIVERSE› = ∑β_j |Ψ_{CLUSTER j›} = ∑α_i |Ψ_WORLD i›.

|Ψ_WORLD i› = |Ψ›_{OBJECT 1} |Ψ›_{OBJECT 2} … |Ψ›_{OBJECT k}    |Φ›.

5. Quantum Parallelism and Many World Interpretation

The power of the new quantum computing model derives from a presumption that it is possible to store and simultaneously manipulate an exponentially-large amount of information in a quantum register. A quantum system of n particles defines an exponential 2ⁿ number of states, it appears that a small amount of computational hardware can behave like a classical parallel computer with an exponential number of processors.

Quantum parallelism arises from the ability of a quantum memory register to exist in a superposition of base states. A quantum memory register can exist in a superposition of states, each component of this superposition may be thought of as a single argument to a function. A function performed on the register in a superposition of states is thus performed on each of the components of the superposition, but this function is only applied one time.

Quantum mechanics imposes a significant restriction: the transformations applied to the quantum register must be unitary. This is necessary because a non-unitary operator is equivalent to performing a measurement and thus will cause a collapse of the superposition.The main idea is that when quantum computers are performing a transition taking as input a superposition of states, like for example the following n qubit register is

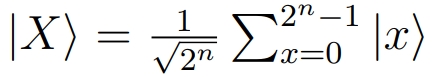
they gain access to many computational worlds—each associated to every possible value of |X_i>—and they are actually performing many simultaneous transitions on each and every one of those states that are part of the superposition. The transition is real in the sense that it is performed in all the different worlds, to which the computation process gain access. The  formal represented by the so called Quantum Parallelism is as follows:

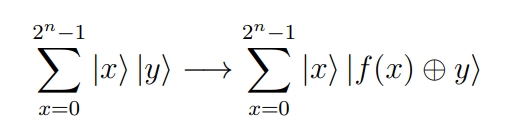
6. Implementation of Quantum Computing with MWI

Standard quantum computing models are based on the paradigm of quantum logic networks, where a sequence of unitary quantum gates form the computational circuit. The key requirements for efficient quantum computing are long coherence time, high scalability, high fault tolerance, ability to initialize qubits, universal quantum gates,  efficient qubit state measurement capability, and faithful transmission of flying qubits.  There are several architectures for implementing quantum computing. Cluster-state quantum computer is one of the key candidate model to run many worlds explanation of quantum computation. The cluster-state quantum computer (QCC) is a universal quantum computer; it can efficiently simulate any algorithm developed within the network model.

An alternative model of circuit model, for scalable quantum computing in which a specific form of a highly entangled multiparticle state, called a cluster state, plays the pivotal role of being a universal resource for quantum computation. To perform a quantum algorithm with a cluster state, individual qubits are measured in a temporal sequence of adaptive single-qubit measurements with classical feed-forward processing of outcomes.  

Source Books:

1. Compassionate Artificial Intelligence: Frameworks and Algorithms by Dr. Amit Ray
2. Compassionate Superintelligence, AI 5.0 by Dr. Amit Ray
3. Quantum Computing Algorithms for Artificial Intelligence By Dr. Amit Ray

References:

1. Duwell, A. The Many-World Interpretation and Quantum Computation. Philos. Sci. 2007, 74,
   1007–1018. 
2. De Witt, B.; Graham, R. The Many-Worlds Interpretation of Quantum Mechanics; Princeton
   University Press: Princeton, NJ, USA, 1973.
3. Deutsch, D.; Jozsa, R. Rapid Solution of Problems by Quantum Computing. Proc. R. Soc. Lond. A
   1992, 439, 553–558.
4. Giacomo Lini, Quantum Parallelism Thesis, Many World Interpretation and
   Physical Information Thesis, Philosophies 2016, 1, 102-110.
5. Michael Cuffaro, Many Worlds, the Cluster-state Quantum Computer, and the Problem of the Preferred
   Basis, Volume 43, Issue 1, February 2012, Pages 35-42.
6. Gelo Noel M. Tabia, Quantum Computing with Cluster State, 2011, Perimeter Institute for Theoretical Physics, Canada.
7.  Will Advances in Quantum Computing Shed Light on Foundational Issues in Quantum Mechanics?